ブログ

４－８　旅人算２（速さ）

【生徒向け解説】
現在準備中

【答え】
基本問題　８時１２分（１２分後）
問題（１）　１８分
（１分に１００ｍずつ近づく）
参考問題）　９０分
（１分に２０ｍずつ離れていき、それが１周（１８００ｍ）になったときに追いつく）

【保護者向け解説】

４－７　余りの数（規則性）

問題
割り算の余りについての問題です。
（１）６で割ると２余り、８で割ると２余る２ケタの数のうち
小さいほうから３番目の数はいくつでしょう？
（２）６で割ると５余り、８で割ると１余る３ケタの数のうち
小さいほうから８番目はいくつでしょう？

基本問題
６で割ると２余る2ケタの数を、小さいほうから３つ答えてください。

【解説】
定番の問題ではありますが、まずはやってみる、に尽きます。
そして、条件が複数あり、すべてに当てはまるものを求めるタイプの問題は、条件１つずつ書き出していくのが基本。（１）であれば「６で割ると２余る数」を書き出していき、そのあと「８で割ると２余る数」を書き出していき、その両方に当てはまる数の規則を見つける、という流れです。
結果的には、（１）は余りが同じなので、最小公倍数に２を足したものになります。参考までに、算数的には「６で割ると２余る数」のうち、もっとも小さい数は８ではなく「２」です。直接、これを問われることはないですが、身につけておくと、より規則が見つけやすくなる場合は多々ありますので、ぜひ。

【答え】
メイン問題
７４　（小さいほうから２６．５０．７４）
２８１（１１３から２４ずつ増えて８番目）

基本問題
１４．２０、２６

映像は、現在準備中

４－５　回転移動（平面図形）

問題
縦３ｃｍ、横４ｃｍ、対角線５ｃｍの長方形ＡＢＣＤを、床に沿って図のように滑らないように、アイエウに来るまで回転させます。
（１）Ｂはア～エのどの点に移動するでしょう？
（２）点Ｂが通ったあと（軌跡）の長さを求めよ。
（参考）点Ｂの通ったあとと、床で囲まれる図形の面積を求めよ。
（※　カナの振り方が不自然ですが、プリントの都合上、一旦このままで）

基本問題
縦３ｃｍ、横４ｃｍ、対角線５ｃｍの長方形ＡＢＣＤを床に沿って、図のように滑らないように
90度回転させます。Ｂが通ったあと（軌跡）の曲線の長さを求めよ。

【解説】
図形の回転移動の問題です。「１点」を中心にして、図形が回転するときは、他の点は、中心から決まった距離のところを動くため、円に沿って動くことになります。その時には、中心からの距離・動いた角度に注目して、長さや面積を求めることになります。
その時にいきなり「全体」を考えるのではなく、中心が変わるところでは、図形を分けて考えることも重要です。今回の問題では、四角形が４つ（回転は３回）あるので、それぞれ１段階ずつ、中心はどこか、中心からの距離はどれくらいか、動いた角度はどれくらいか、としっかり気を付けながら、解いてもらえればと思います。

あわせて、応用ですが、床の上を「円」が転がる場合、円の中心は水平に動くというのも合わせて、身につけておきましょう（だからこそ、電車の座席は上下の動きをしないのです）

【答え】
メイン問題
（１）エ
（２）18.84㎝

基本問題
6.28ｃｍ（半径４ｃｍで中心角90度のおうぎ形）

映像は現在準備中

３－８　円グラフ・棒グラフ

問題

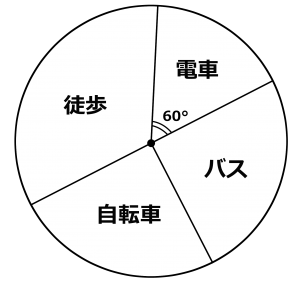
図は１学年３００人がどのように学校に通っているかを円グラフで表したものです。ただし電車とバスのように2つ以上の方法で通う生徒はいないものとします。
（１）　電車で通っている人は何人でしょう？
（２）　バスで通っている人は７５人です。バスの部分の中心角は何度でしょうか？
（３）　これを全体２０ｃｍの帯グラフにすると、電車の部分は何ｃｍになるでしょう？

基本問題
1６0人にアンケートをとったら、「はい」が80人、「いいえ」が80人でした。
結果を円グラフに表すと、どのようになるでしょう？グラフを描いてみてください。

【解説】
全体のうち、注目しているものがどれくらいか、という「割合」を目で見てわかりやすく表すための「円グラフ」「帯グラフ」の問題です。
円グラフの場合は、円全体の中心角360度を100％（10割）とするため、3.6度が1％、または1度が360分の100％として考えるのが王道とされています。
しかしながら、メイン問題の（１）については60度分なので、全体の16.666…％（100÷6）となってしまいます。そういうときのために、割合は「分数」で考える習慣をつけておくとよいでしょう。その場合は、全体360度のうちの60度分は6分の1となり、300人の6分の1で、300÷6で50人と出すことができます。
また帯グラフの場合は、全体が帯の長さ（（３）では20㎝）のため、問題ごとに1％分がどれくらいか、注目しているものは全体の何分の何か、などを考えていく必要があります。
またグラフは、公立一貫校での資料としての出題も多く、その中で計算問題として課されることも多いので、しっかり身につけておきましょう。

【答え】

メイン問題
（１）50人
（２）90度
（３）3分の10㎝

基本問題
略

映像準備中

３－７　順列・組み合わせ（通りの数）

問題
６人の生徒から、下のように代表を選びます。
（１）班長・副班長を選ぶ方法は何通りでしょうか？
（２）２人の掃除当番を選ぶ方法は何通りでしょうか？

基本問題
３人の生徒（たこくん・いかくん・かにくん）から、２人を選ぶ方法は何通り？

【解説】
通りの数（順列・組み合わせ)の問題です。
基本的には、数え損ねたり、同じものを２回数えたりすることがないように「樹形図」を書くのが、まず身につけたい方法です。
そして樹形図を書いていく中で、規則性が見えたら計算に、そうでなければ最後まで書ききるということを繰り返してほしいと思います。いきなりかけ算の式を書き始めるのは、超上級者になってから。少なくとも、樹形図を思い浮かべるところから始めましょう。

またメインの問題では、順番も意識する「順列」と、順番を意識しない「組み合わせ」の区別ができるかどうかを出題しました。慣れてきた後でも、この区別ができていないことでの失点が多く見られますので、ご注意を。
迷った時には、「「１－２」と「２－１」は別物か？」のように、具体的な例で考えてみてください。

【答え】

メイン問題
（１）３０通り
（２）１５通り

基本問題
３通り

映像は現在準備中