カテゴリー: 受験算数

５－５　回転移動（四角形ー円）

問題

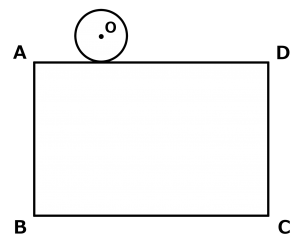
ＡＢ５ｃｍ、ＡＤ８ｃｍの長方形の周りを、半径１ｃｍの円が転がりながら１周します。
（１）ＡＤ上で円が１回転する間に、円の中心Ｏは何㎝進むでしょう？
（２）円が長方形を１周する間に、円の中心Ｏは何㎝進むでしょう？
（３）長方形を１周するまでに、円が通過した部分の面積を求めよ。

基本問題（復習―おうぎ形の周と面積）
半径６ｃｍ、中心角が１３５度のおうぎ形について考えます
（１）この図形の周の長さは何ｃｍでしょう？
（２）この図形の面積は何㎠でしょう？

【解説】
円が図形の周りを回転していく問題です。
円が直線状を動く時には、その中心は直線（床と平行）に動くということ、そして、１点を中心に回転する「角（頂点）」の部分では、円の中心は、「角を中心とする円」として動くこと、を利用していく問題です。
またイメージですが、（１）のように円が１回転する間に、円と床が接しながら移動していくため、ちょうど円の１周分だけ床の上を動く、ということも身につけておくとよいかと思います。
４－５の回転移動とセットにして抑えておきましょう！

【答え】
問題
（１）　６．２８ｃｍ
（２）　２９．１４ｃｍ
（３）　６４．５６平方センチメートル
基本問題
（１）　２６．１３ｃｍ（弧は14.13㎝）
（２）　２１．１９５平方センチメートル

映像準備中

５－４　整数の性質（割れる回数）

問題
１×２×…×１０の答えを３で割っていくことにします。
さて、何回割り切れるでしょう？

基本問題
１８を素因数分解してください

【解説】
数の性質の問題です。「３で割り切れる」ためには、その数に「×３」が含まれている必要があり、また、割れる回数も「×３」の個数で決まる、ということを使う問題です。今回は１から１０までの間に、３そのものは１個しかありませんが、６は「２×３」と、「×３」を含んでいますし、９については「３×３」のように、「×３」を２個含んでいます。
また応用ですが、１から１００までのかけ算などになった時には、「×３」を持つ数、つまり３の倍数はいくつあるのか、そのうちに、「×３×３」を持つ数である９の倍数はいくつあるのか、などと考えていくことになります。また機械的に計さんで出す方法も知られていますが、使う場合は、なぜそのやり方で出せるのかを、説明できるようにしておいてほしいと思います。

【答え】
問題
４回（５回目で割り切れなくなる）

基本問題
２×３×３

映像準備中

５－３　集合とベン図

問題
４０人のクラスで、カレーとハンバーグの好き嫌いについてアンケートを取りました。
カレーが好きと答えたのは２８人、ハンバーグが好きと答えたのは２５人、両方とも嫌いと答えたのが６人でした。さて、両方とも好きと答えたのは何人でしょう？

基本問題
４０人のクラスで、たこといかの好き嫌いについてアンケートを取りました。
たこが好きと答えたのは２０人、いかが好きと答えたのは１２人、両方とも好きと答えたのが５人でした。さて、両方とも嫌いと答えたのは何人でしょう？

【解説】
いわゆる集合算の問題です。集合の問題は、まず「ベン図」か「表」を描くところから始めます（注）
そのうえで今回のように、「たこの好き嫌い」「いかの好き嫌い」のような項目が2つの場合は、全部で4つの仲間に分けられることになること、そして「たこが好き」の中には、「たこが好きで、いかが好き」「たこが好きで、いかが嫌い」という2つが入っていることを意識すると、見通しが立てやすくなります。

（注）基本的に「ベン図」と「表」のどちらを選ぶかは好みで良いが、全体像を得るだけならベン図、細かい計算が必要なら表のほうがわかりやすいです。また項目が3つになった場合は、表では描けないのでご注意を。

【答え】
メイン問題
１９人
基本問題
１３人

映像準備中

４－８　旅人算２（速さ）

【生徒向け解説】
現在準備中

【答え】
基本問題　８時１２分（１２分後）
問題（１）　１８分
（１分に１００ｍずつ近づく）
参考問題）　９０分
（１分に２０ｍずつ離れていき、それが１周（１８００ｍ）になったときに追いつく）

【保護者向け解説】

４－７　余りの数（規則性）

問題
割り算の余りについての問題です。
（１）６で割ると２余り、８で割ると２余る２ケタの数のうち
小さいほうから３番目の数はいくつでしょう？
（２）６で割ると５余り、８で割ると１余る３ケタの数のうち
小さいほうから８番目はいくつでしょう？

基本問題
６で割ると２余る2ケタの数を、小さいほうから３つ答えてください。

【解説】
定番の問題ではありますが、まずはやってみる、に尽きます。
そして、条件が複数あり、すべてに当てはまるものを求めるタイプの問題は、条件１つずつ書き出していくのが基本。（１）であれば「６で割ると２余る数」を書き出していき、そのあと「８で割ると２余る数」を書き出していき、その両方に当てはまる数の規則を見つける、という流れです。
結果的には、（１）は余りが同じなので、最小公倍数に２を足したものになります。参考までに、算数的には「６で割ると２余る数」のうち、もっとも小さい数は８ではなく「２」です。直接、これを問われることはないですが、身につけておくと、より規則が見つけやすくなる場合は多々ありますので、ぜひ。

【答え】
メイン問題
７４　（小さいほうから２６．５０．７４）
２８１（１１３から２４ずつ増えて８番目）

基本問題
１４．２０、２６

映像は、現在準備中